光栅化部分课程笔记

现代计算机图形学入门 - 2020春季 - 闫令琪UCSB

课程主页
课程论坛
课程地址

实验/作业环境

虚拟机下搭建环境

# Ubuntu 18.04
sudo apt-get install libopencv-dev
sudo apt-get install libeigen3-dev

向量与线性代数

向量点乘

• 求夹角余弦Cosθ
• 通过点积结果正负判断两个向量是否同向(Forward/Backward)

向量叉乘

• 通过叉积结果z分量的正负判断向量的左右关系，AXB>0则B在A左边（右手定理）。这个特性可以应用于判断点是否在三角形内。

变换（二维与三维）

线性变换：对称、旋转、缩放、切变

图形的线性变换均可以用一个相同维度的变换矩阵左乘表示x' = Mx

其中x表示某个点（或向量），如果是二维，则M是2X2矩阵。
注意在这样的表述下，平移不属于线性变换，因为变化的常量与x,y无关。

齐次坐标

为什么引入齐次坐标？

为了解决上面平移不属于线性变换，无法用矩阵左乘来表示的问题，所以引入了齐次坐标。自此，所有渲染过程用到的变换操作都可以用一个矩阵左乘来表示了。注意矢量平移前后仍为同一矢量，且为了保证齐次坐标下运算的一致性（两个点相减等于一个新的矢量），所以二维向量的齐次坐标第三位是0。

齐次坐标统一后的线性变换表示：

齐次坐标下可以将线性变换与平移写成一个变换矩阵，代表着仿射变换，先做线性变换再平移。
三维如上类推即可。

变换（模型、视图、投影）

Rodrigues’ Rotation Formula

三维环境下的任意一个旋转都可以拆解成绕三个轴的简单旋转组合。以下公式为绕过原点旋转轴$n$旋转$\alpha$角度，具体的推导可以参考:

\[R(n, \alpha) = cos(\alpha)I + (1 - cos(\alpha))nn^T + sin(\alpha)\begin{pmatrix}0 & -n_z & n_y\\\\n_z & 0 &-n_x\\\\-n_y & n_x & 0\end{pmatrix}\]

绕不经过原点的轴旋转类似二维可以拆解为： 平移使轴经过原点计算平移矩阵\(T\)，计算旋转矩阵\(R\)，平移回原来的位置\(T^-\):

\[M_{T^-}M_RM_T\]

视图/相机变换

把相机变换至规定的位置和方向，即处于原点，向$-Z$方向看，上方向为$Y$轴正方向，这个变换矩阵叫做视图变换。

非常有意思的是，旋转矩阵是正交矩阵，其可逆等于其转置。这时候用来求上图中的$R_view$就非常方便了。

投影变换

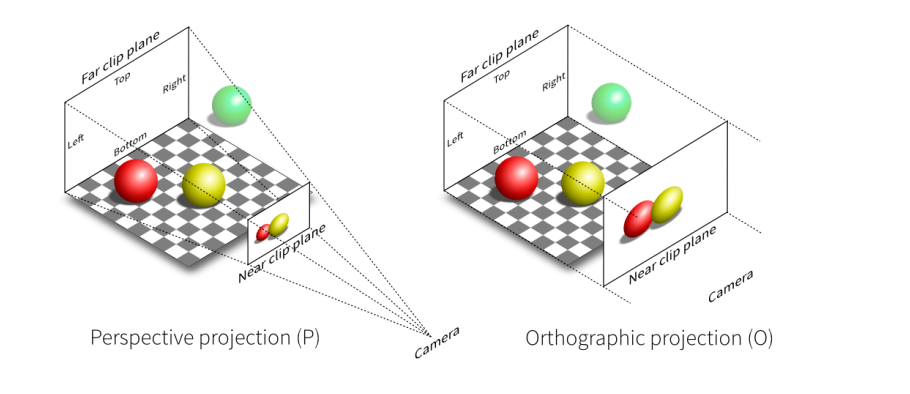
正交投影

更多的用于工程制图。

透视投影

更多贴近于真实的人眼，有近大远小现象，应用最广泛的投影变换。

光栅化Rasterization

相机宽高比Aspect Ratio与垂直视距角度 fovY

建立屏幕像素坐标系

Pixels’ indices are from (0, 0) to (width - 1, height - 1)

视口/屏幕变换

把之前投影的结果$(-1,1)^3$经过变换映射到屏幕像素坐标系中。

不同的显示设备

CRT-阴极显像管显示器（高中物理） LCD-液晶显示器 LED-发光二极管 OLED-有机发光二极管 Electrophoretic-电泳显示(kindle电子墨水屏，刷新率低)

光栅化（抗锯齿与深度测试）

抗锯齿（反走样）Antialiasing

采样导致的锯齿现象属于Sampling Artifacts（Errors/Mistakes/Inaccuracies）的一种。比如人眼观察高速的车轮轮毂有时会看到倒转也属于走样，这是人眼或相机在时间上的采样导致的。毕竟是连续变离散，当采样速率追不上信号变化的速率就会导致走样，这是采样原理导致的不准确性。

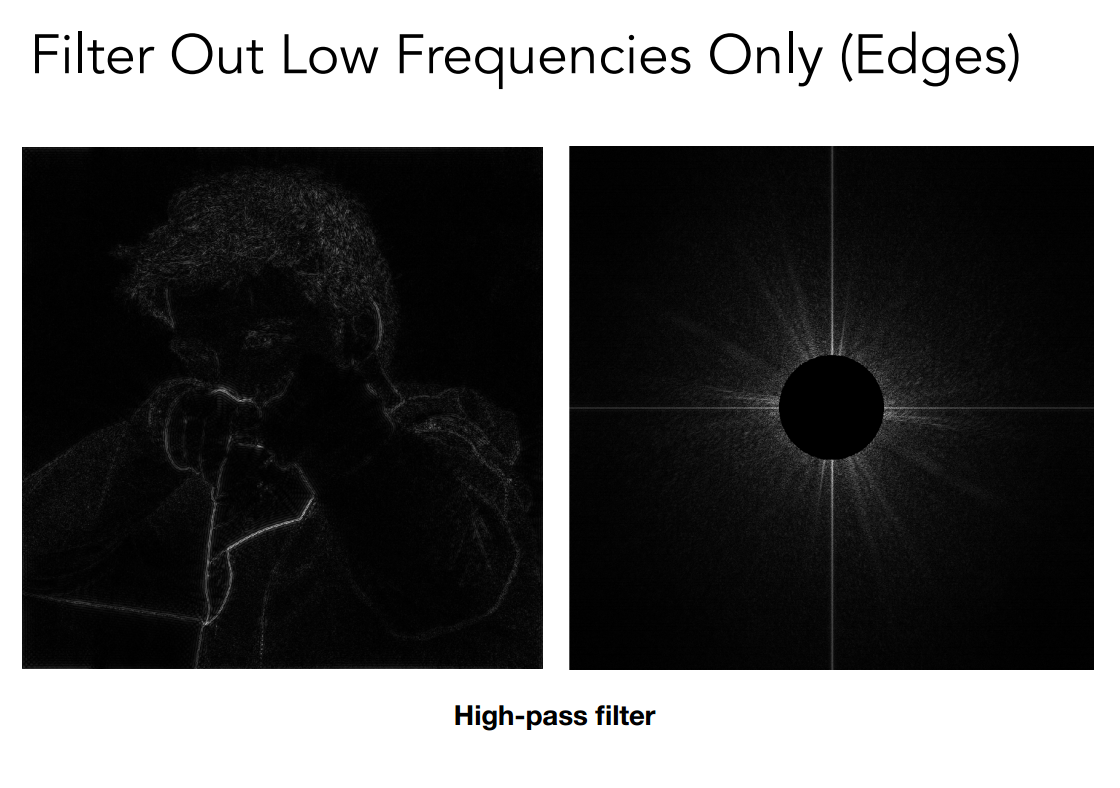
Filtering 滤波： 用于过滤特定频率的信号。在图像中，高频一般是灰度变化较大的边界，也是锯齿容易产生的位置。

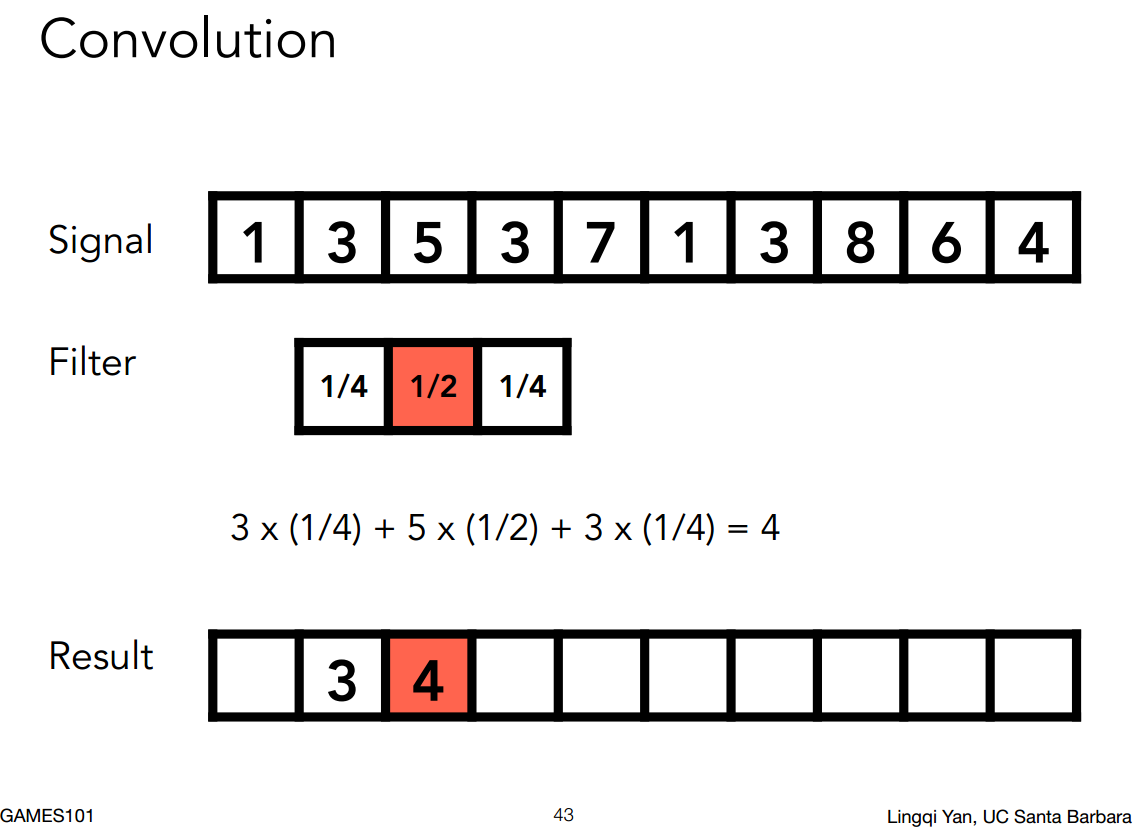
Convolution 卷积：通过一种计算方式，将某个信号与其周围的信号取平均，得到一组变化平滑的新信号。

所以抗锯齿要做的事情是在采样前，对三角形的每个像素进行box-blur，卷积操作求平均。

MSAA（Multisample Antialiasing） 2x2 4x4 8x8

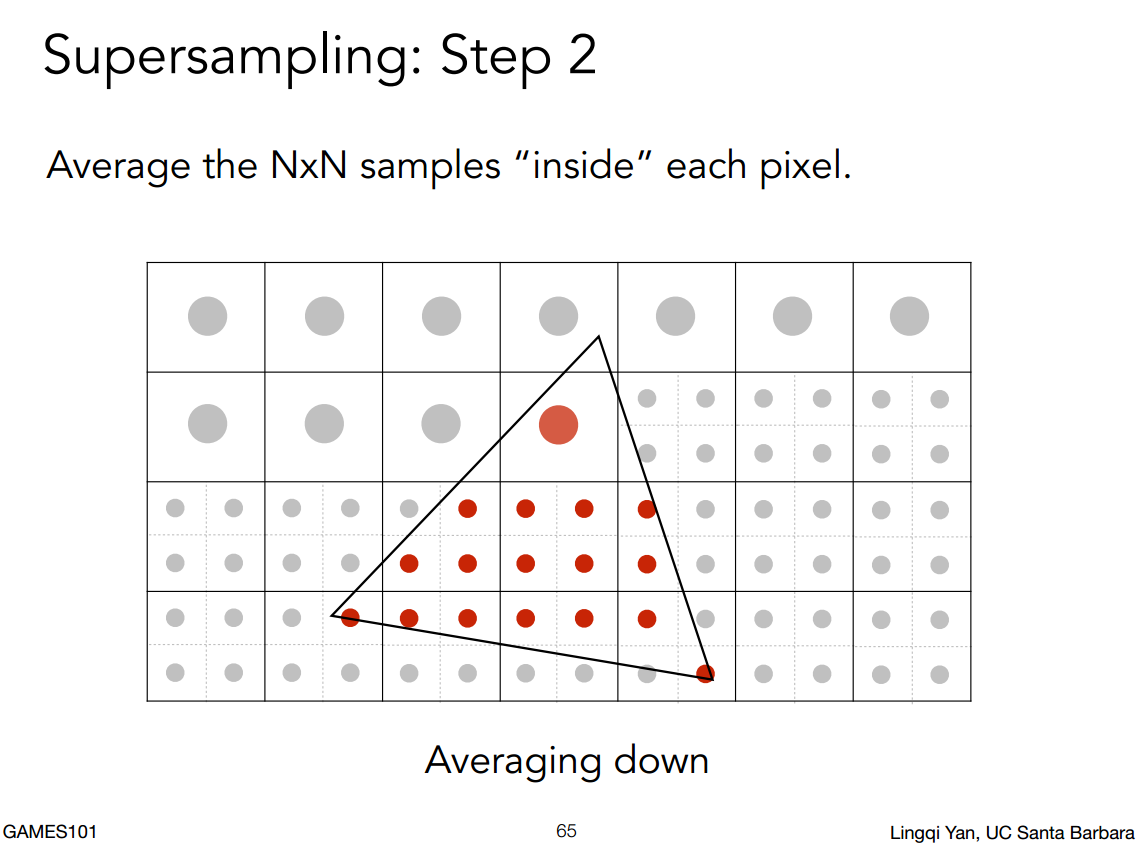
NxN的MSAA意味着在一个像素内取N个均匀分布的采样点，计算一个像素在三角形内采样点的比例并求出该像素颜色的平均值，作为该像素的颜色。

拓展 FXAA TAA 当下广泛应用的抗锯齿的方案

• FXAA：在图像层面做的抗锯齿，不是在采样上做文章。效率很高效果也很好。
• TAA：复用上一帧的信息，效率很高。

深度测试

着色（光照与基本着色模型）

Blinn-Phong反射模型

$\vec{light}$着色点（shading point）指向光源的单位向量 $\vec{normal}$着色点法向量（单位向量） $\vec{view}$着色点指向视角的单位向量

漫反射

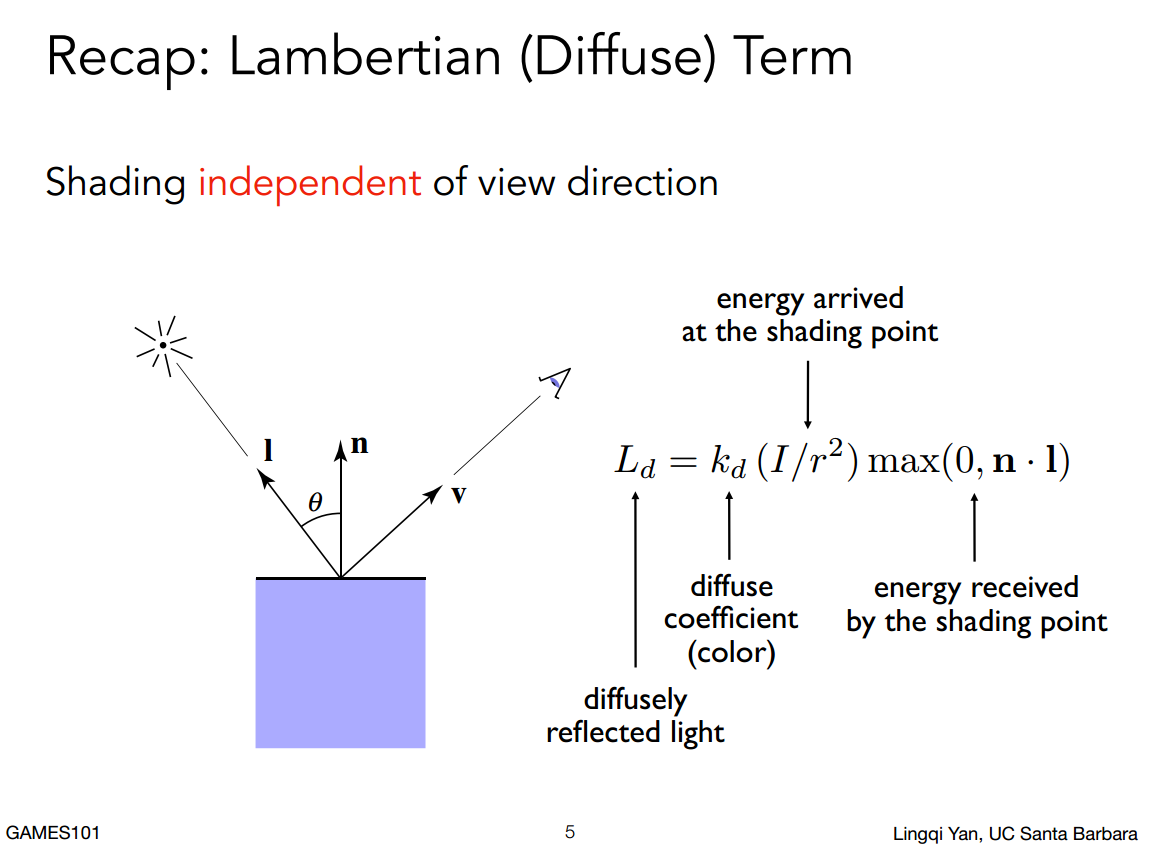
与观察视角无关的一个光照公式，与物体材质的漫反射系数、光照强度、着色点到达光源的距离、着色点吸收的光照能量（与$\vec{light}$，$\vec{normal}$夹角有关）有关。

高光

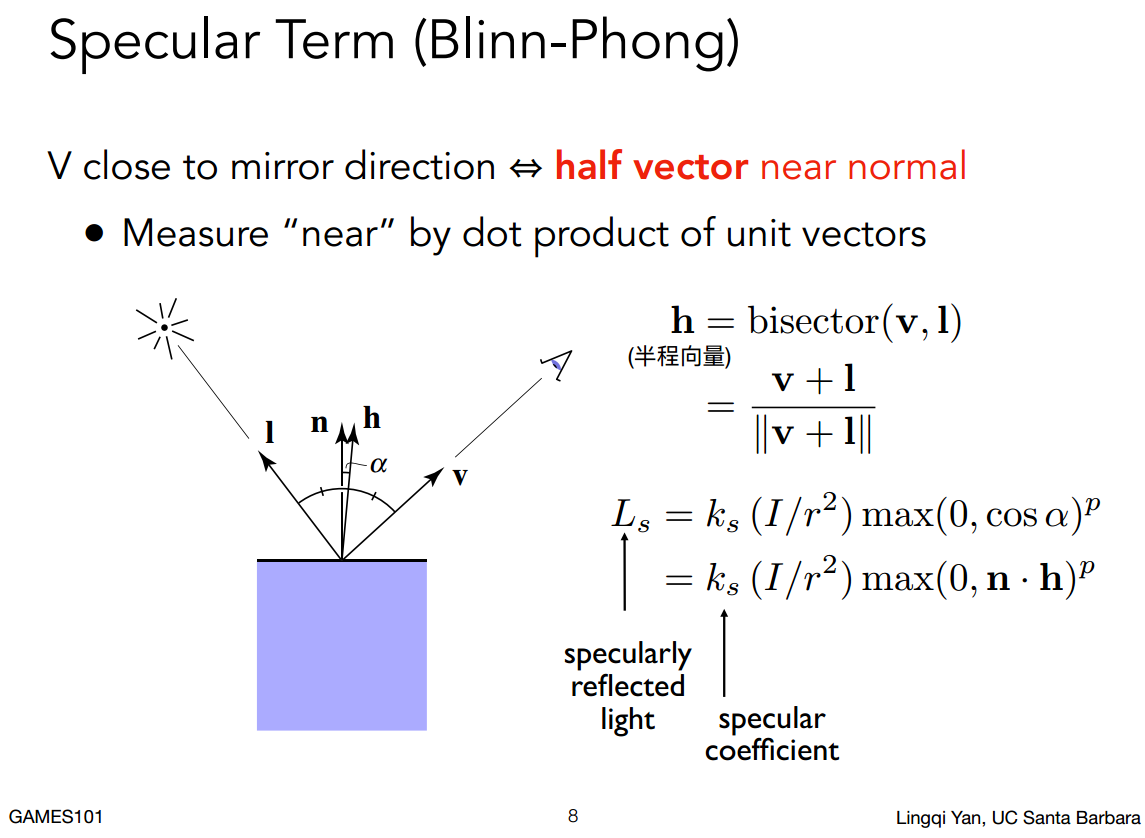
观察方向与镜面反射后的光照方向接近时可以看到高光。取巧可以借助$\vec{light}$与$\vec{normal}$的半程向量$\vec{half}$和$\vec{normal}$是否接近来判断（点乘）

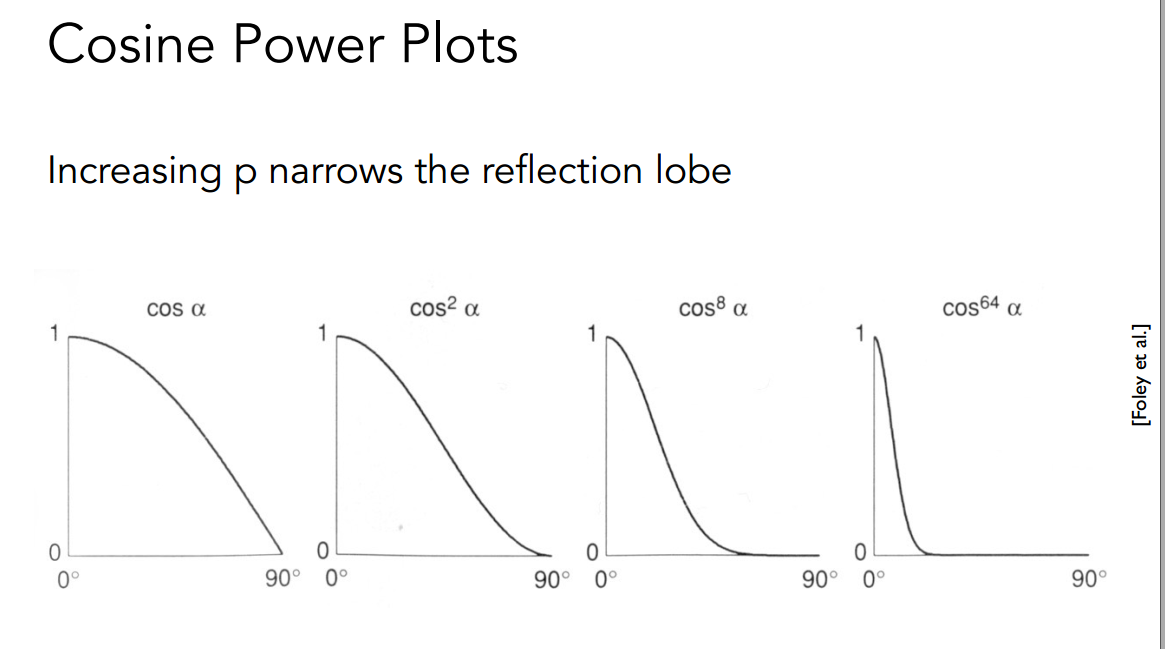
Blinn-Phong的高光模型属于经验简化模型，不考虑光照能量的吸收情况所以不会有$n·l$。另外夹角余弦上的指数p是用于优化余弦函数，使其更贴近现实，当夹角稍微大一点就看不到高光。

环境光

$L_a = k_aI_a$

假设所有点接收到的环境光强度$I_a$ 是相同的，且$L_a$和$\vec{normal}$，$\vec{view}$均无关。

Blinn-Phong模型

三种光照叠加起来即为Blinn-Phong模型。

着色（着色频率、图形管线、纹理映射）

着色频率

Flat shading逐三角形着色， Gouraud shading逐顶点着色， Phong shading逐像素着色三种着色频率

图形管线/实时渲染管线

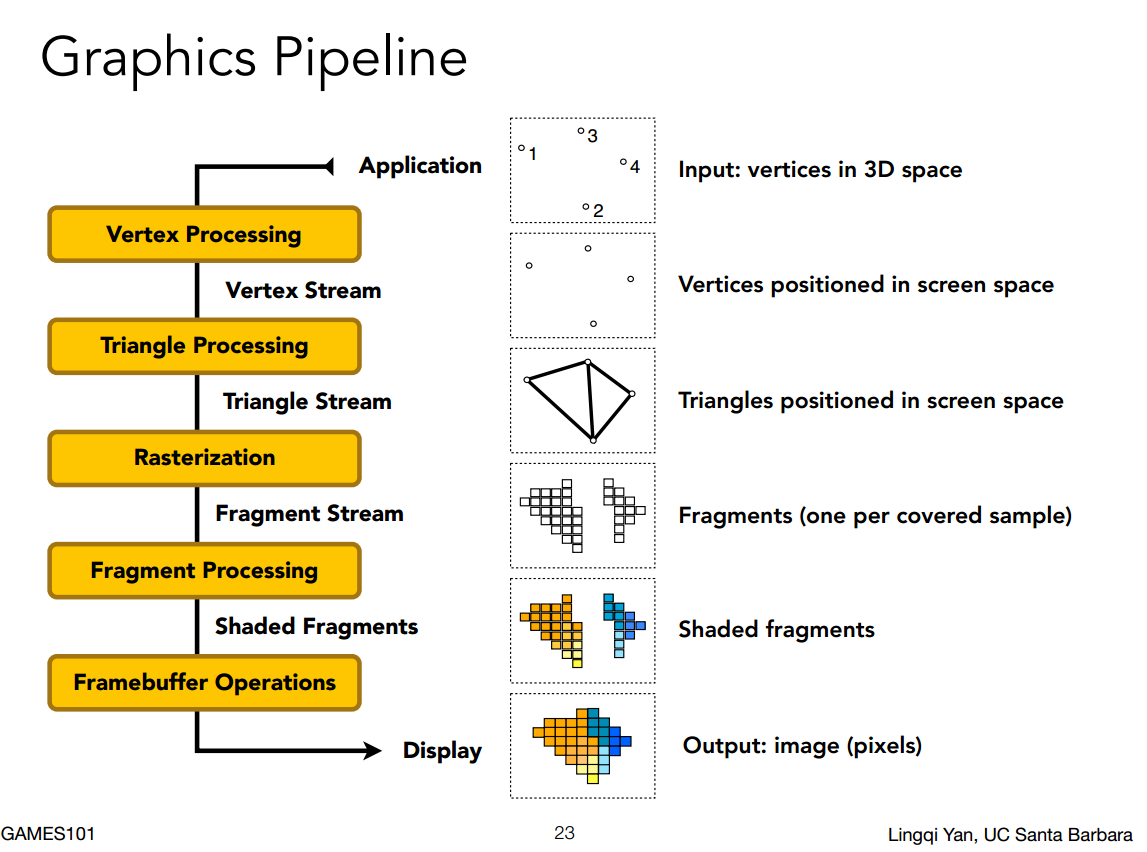
由GPU硬件负责全部的操作。

Texture Mapping

• 任何三维物体表面都可以展开成二维（地球仪与世界地图）
• 纹理就是三维物体表面的二维映射
• 具体怎么映射生成的纹理，是由模型制作工具来完成的
• 每个三维中的三角形对应纹理的坐标$(u,v)$
• 纹理设计应该允许横向纵向的重复应用
• 纹理应用也涉及到插值

着色（重心坐标插值、纹理映射、纹理应用）

三角形插值：重心坐标 Interpolation Across Triangles: Barycentric Coordinates

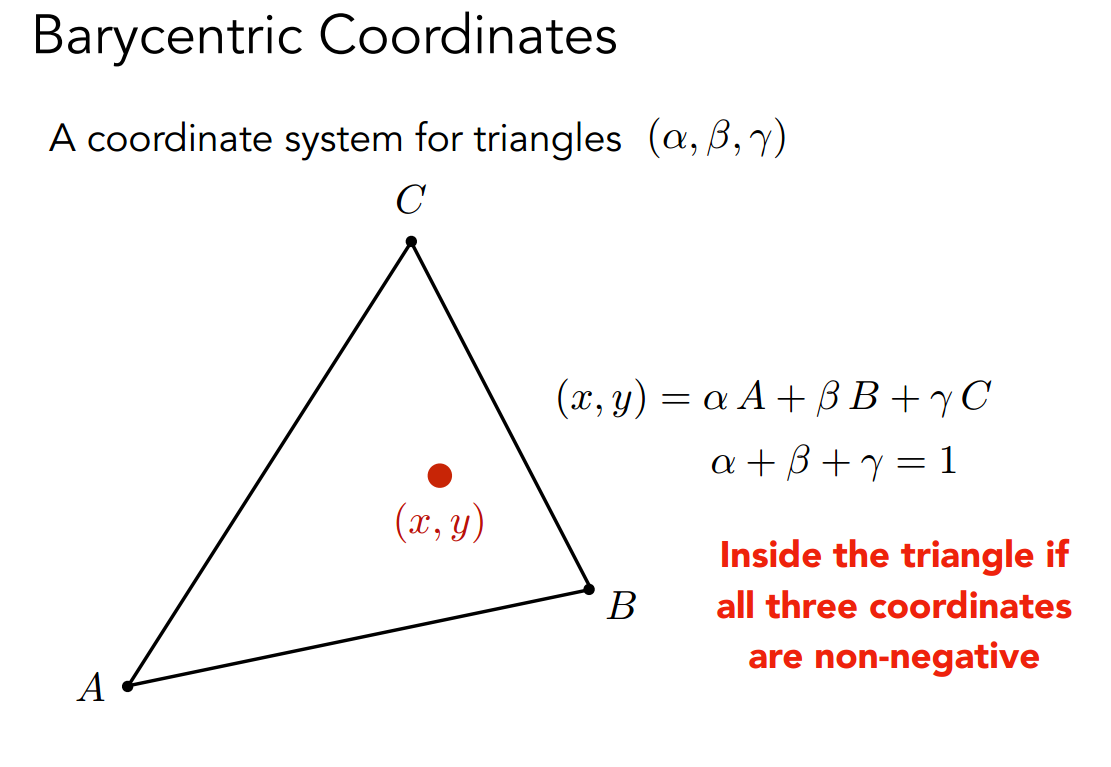
重心坐标$(\alpha,\beta,\gamma)$并不会在三维投影到二维后不变

纹理映射

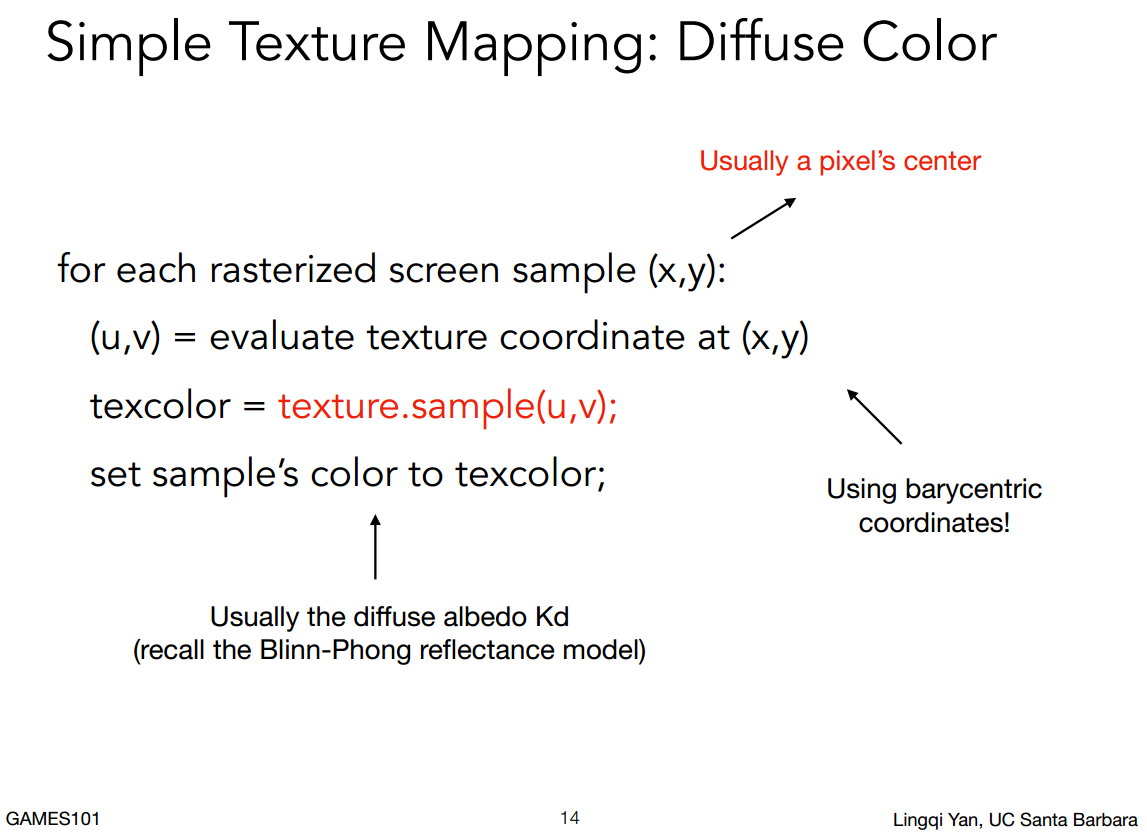
找到某个点的插值uv -> 找到纹理中对应uv的颜色 -> 应用该颜色至该点的漫反射系数Kd。

双线性插值

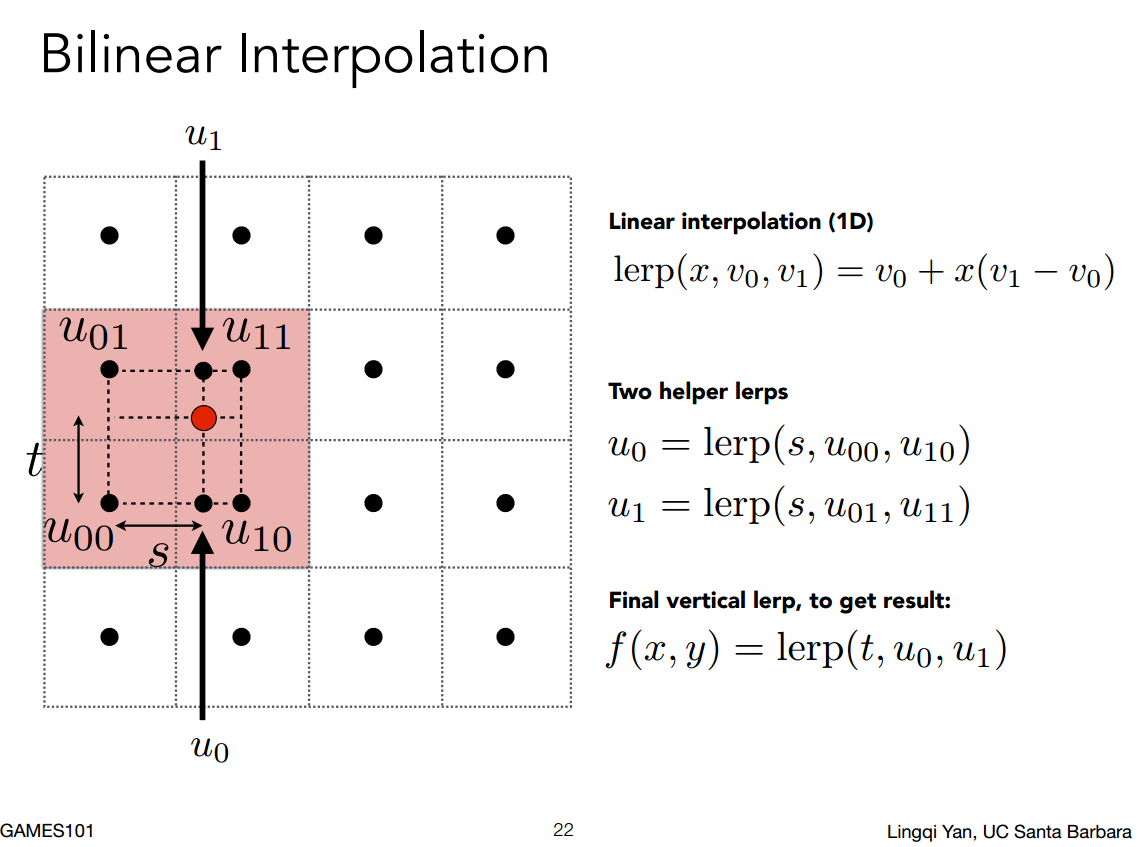
当纹理图很小时，渲染的多个像素可能都被纹理映射到同一个uv上去，为了渲染结果能够平滑无锯齿，此时需要在texture.sample(u,v)时对纹理结果进行u,v两个方向上的插值得到一个加权平均纹理值。

Bicubic使用的是附近16个texel来做加权平均，以更高的计算开销来获得更好的效果

范围查询 - Mipmap - 三线性插值

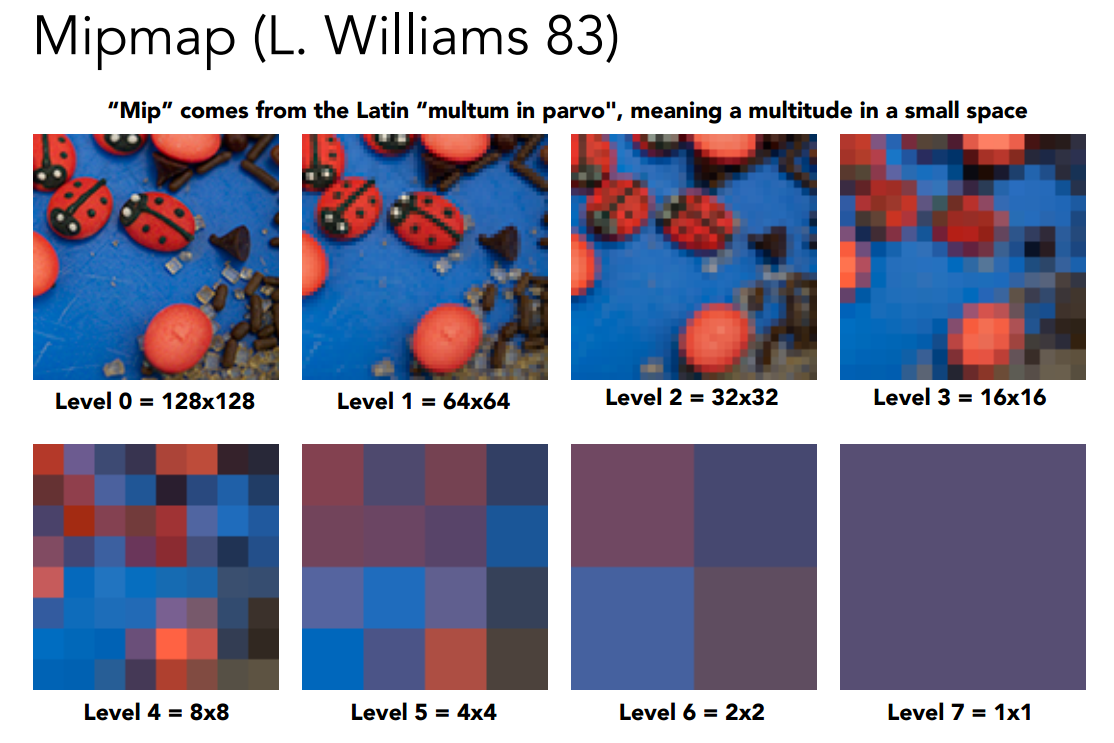
当纹理图很大时，一个像素可能会覆盖纹理很大范围。如果此时仍然只采样中心点坐标的纹理值会导致走样，所以需要计算该像素覆盖范围内的平均值。Mipmap是一个预生成的用于快速查询某个范围纹理平均颜色的纹理图，最多付出额外1/3的显存开销。

各向异性过滤

一个用来解决mipmap引出的over blur过度模糊的技术，类似变种Mipmap技术，预生成不等宽高比的纹理图用于采样。最多付出额外3倍的显存开销。

纹理应用

在现代GPU中，纹理不局限为一张贴图，而是GPU内存中可以用于做查询（包括范围查询、点查询）的一块数据。

texture = memory + range query(filtering)

因此纹理有以下应用

环境光照

可以用纹理描述环境光照，渲染到物体上可以表现出反射。（金属球）

凹凸/法线贴图 Bump/Normal mapping

通过法线贴图映射改变每个像素的法线方向，从而影响着色，就可以在某个光滑模型表面实现出凹凸质感（即不改变几何模型）。

位移贴图 Displalcement mapping

同法线贴图，但是是真的改变几何模型顶点。更加真实，细节更丰富，并且在阴影上不会露馅。

预计算shading结果

比如记录环境光遮蔽信息的纹理贴图

三维纹理与体积渲染 3D Textures and Volume Rendering

Geometry 几何

如何描述各种形态、复杂的物体（汽车引擎、毛发、丝绸、水、草、显微镜下的微生物、树）与复杂的场景（城市、大场景远景）是几何涉及的研究内容。

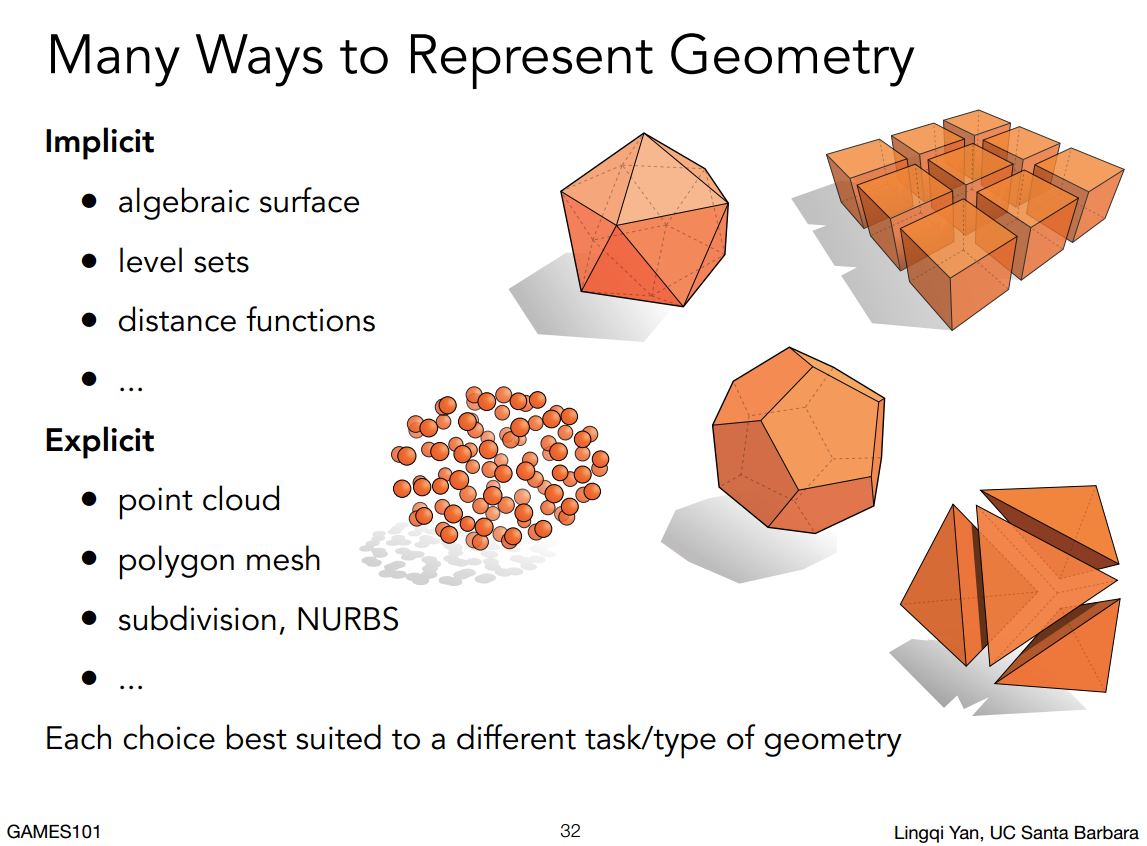
隐式(Implicit)几何与显式(Explicit)几何： 隐式几何表示顶点之间的关系，不给实际的点数据。比如球体表面可以定义为$x^2+y^2+z^2=1$。隐式的$f(x,y,z)$函数可以简单的判断某个特定的点是否在物体内（代入算小于0则在物体内部，0在物体表面，大于0在物体外部），但是隐式难以找出所有在物体上的点。显示几何则通过给出所有点的坐标或者通过参数映射的方式遍历二维映射出三维中所有点坐标，但是判断点在物体内外变得困难。

Implicit Geometry 隐式几何

• CSG(Constructive Solid Geometry)是隐式几何的一种，是通过计算一些基础几何（圆柱、球）的布尔运算（交、并、差）拼凑出复杂几何。
• SDF(Signed Distance Functions)也是隐式几何的一种，用来表示空间中的任意一点到物体表面的最小距离。可以计算SDF函数值为0的点来算出边界，也可以在blending混合阶段用于计算边界的混合（水滴落入水中溅起的水花）。
• Level Sets水平集也是使用这种原理，只是表示的方式不太一样（表示方式类似等高线），可以通过取特定值来找出对应几何边界。
• Fractals（分形，自相似，类似递归）

隐式几何的特点：

• 简单的描述（函数）
• 容易查询特定点在几何内外
• 易于计算光线与表面求交（光线追踪）
• 对于一些简单的形状可以精确的描述，不会有采样错误
• 易于处理物理拓扑结构的变化（水）
• 很难处理复杂形状的模型（所以引入显式几何）

Explicit Geometry 显式几何

• Point Cloud 点云：list of points (x,y,z)。
  • 复杂的模型需要高密度的点云
  • 三维扫描的输出就是点云
  • 点云通常会被转换成polygon mesh
  • 点云的应用不是很广泛
• Polygon Mesh 多边形面：存储顶点与多边形（三角形或四边形）
  • 应用最为广泛
  • 建模软件的输出
  • Wavefront Object File（.obj）：一个文本文件用于定义顶点、法线、纹理坐标及其连接关系。广泛用于图形学研究

Curves 曲线

Bezier Curve 贝塞尔曲线

通过若干个点定义一条唯一的光滑的曲线，操纵控制点的位置可以得到任意一条连续光滑的曲线。可以通过de Casteljau算法来画这个曲线。

先考虑三个顶点的情况（二次贝塞尔曲线）：

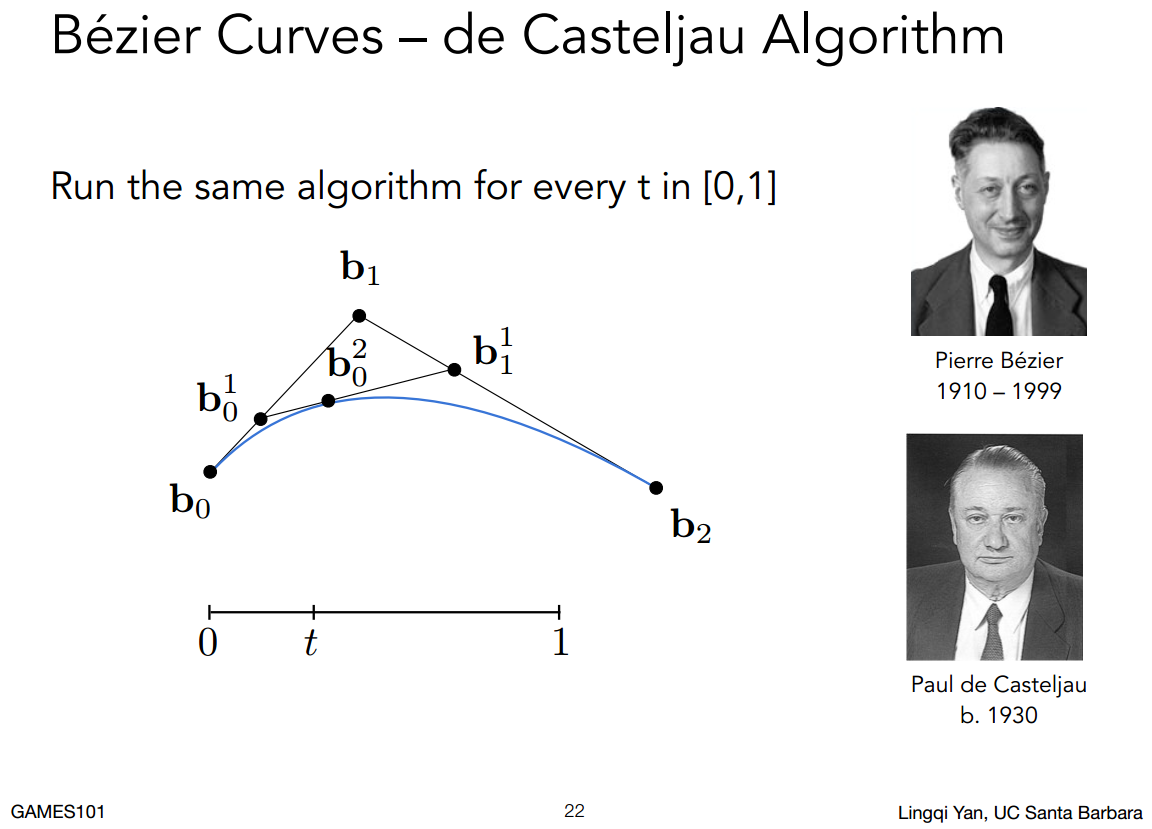
再考虑四个顶点的情况，递归线性插值来算出曲线上的点的具体位置：

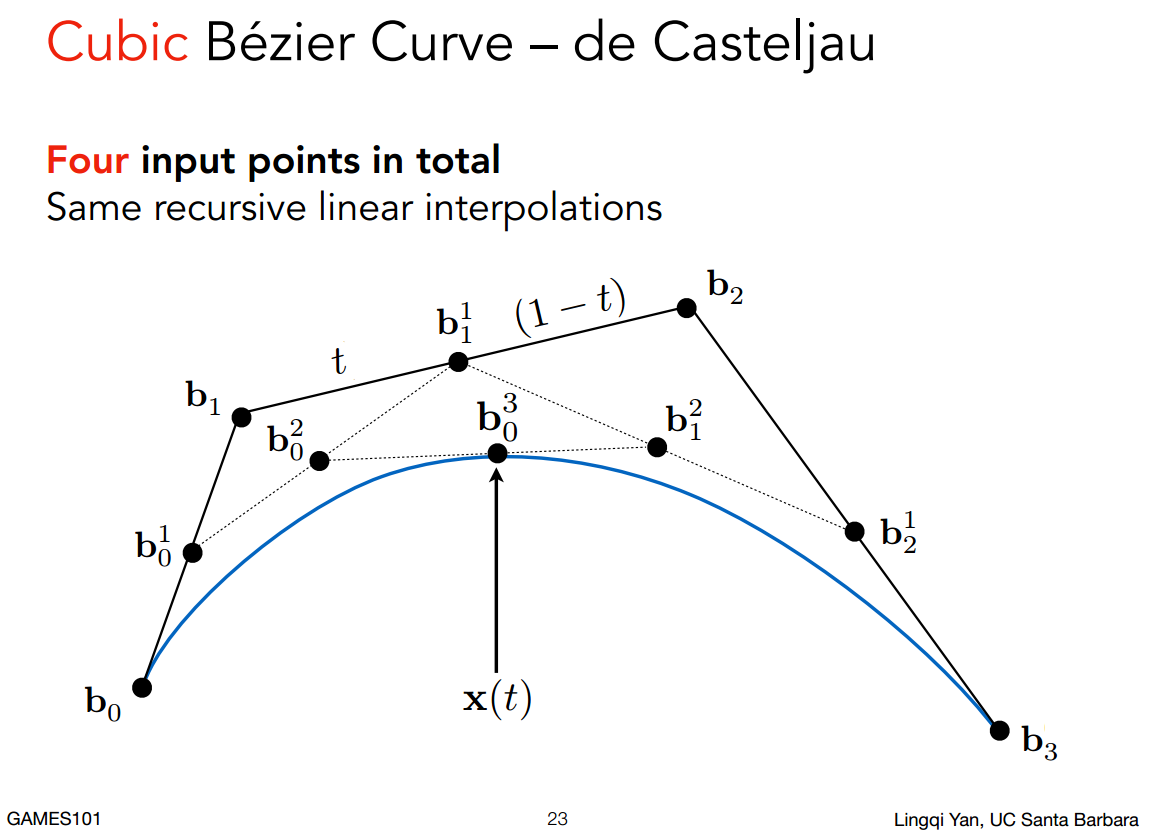
根据线性插值可以推导出N阶（即N-1个控制点）的贝塞尔曲线的代数表示：

具体的二次贝塞尔曲线（控制点b0 b1 b2）代数表达式：

$b_0^2(t)=(1-t)^2b_0+2t(1-t)b_1+t^2b_2$

三次贝塞尔曲线（控制点b0 b1 b2 b3）代数表达式：

$b_0^3(t)=b_0(1-t)^3+b_13t(1-t)^2+b_23t^2(1-t)+b_3t^3$

Piecewise Bezier Curve 逐段贝塞尔曲线

高阶的贝塞尔曲线非常难控制（因为线性插值了所有控制点的信息）。所以为了更方便的描述一些精巧的曲线，可以通过绘制几段贝塞尔曲线然后拼接，即逐段贝塞尔曲线（常用三阶贝塞尔曲线，即4个控制点来绘制）。这个方法广泛用于字体、路径、幻灯片。

逐段贝塞尔曲线需要考虑连续光滑性，分为C0连续性（值连续）与C1连续性（导数连续）。

其他曲线

• Spline 样条曲线
• B-splines B样条曲线，具备曲线局部性（类似逐段贝塞尔）
• …

Surfaces 曲面

Bezier Surfaces 贝塞尔曲面

在两个方向上都做一次贝塞尔曲线的绘制。

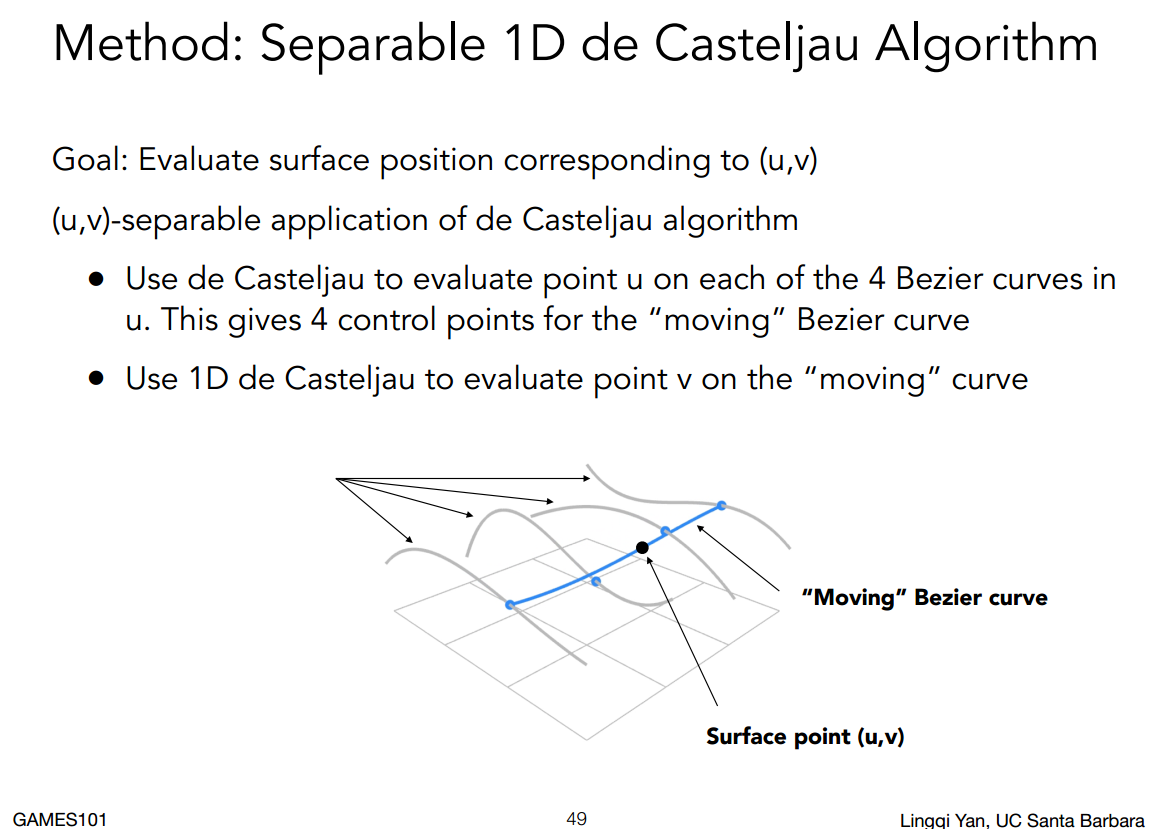
Mesh Operation 网格处理

Subdivision细分、Simplification简化、Regularization规范。

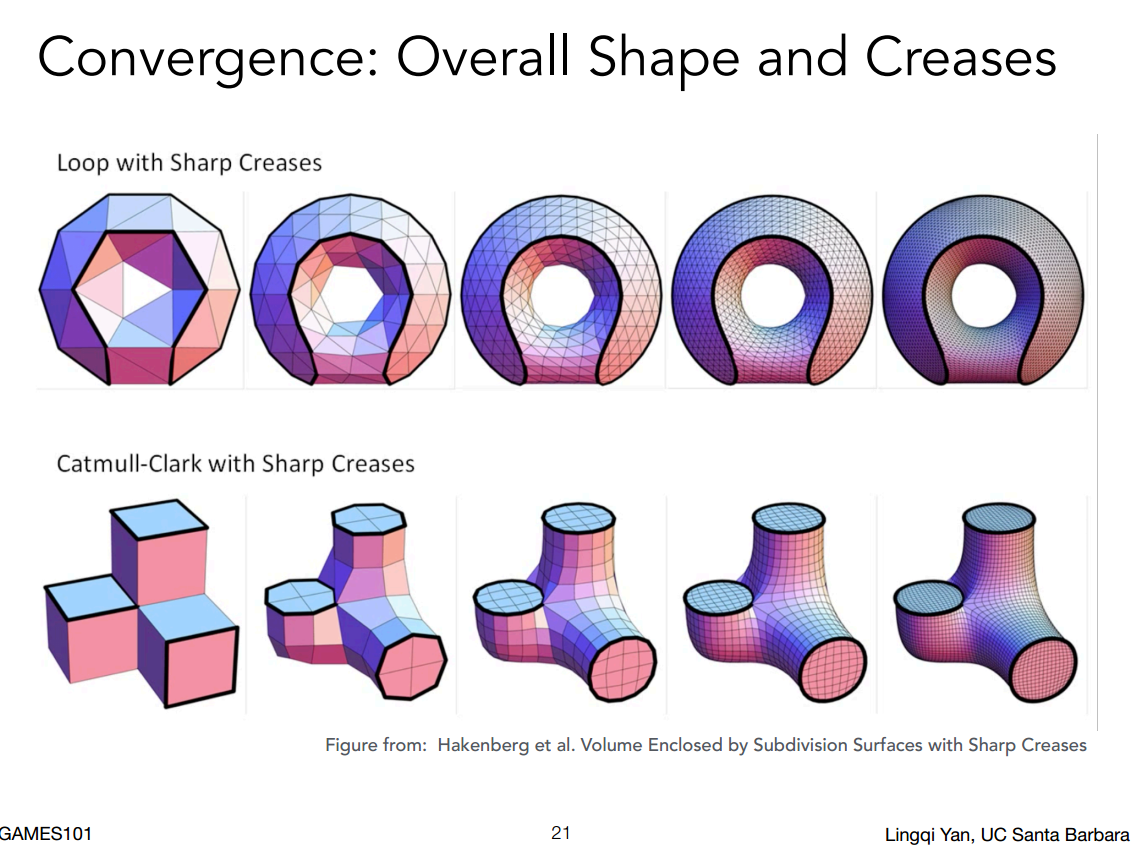
Mesh Subdivision 网格细分

• Loop Subdivision：一种三角形网格细分的算法。把1个三角形各取中点相连，细分成4个，同时更新新、旧各顶点的位置（加权平均），使模型变得光滑圆润
• Catmull-Clark Subdivision：一种通用网格细分算法。原理相同都是添加新的点，只不过生成四边形网格，同时加权平均计算新、旧顶点的位置

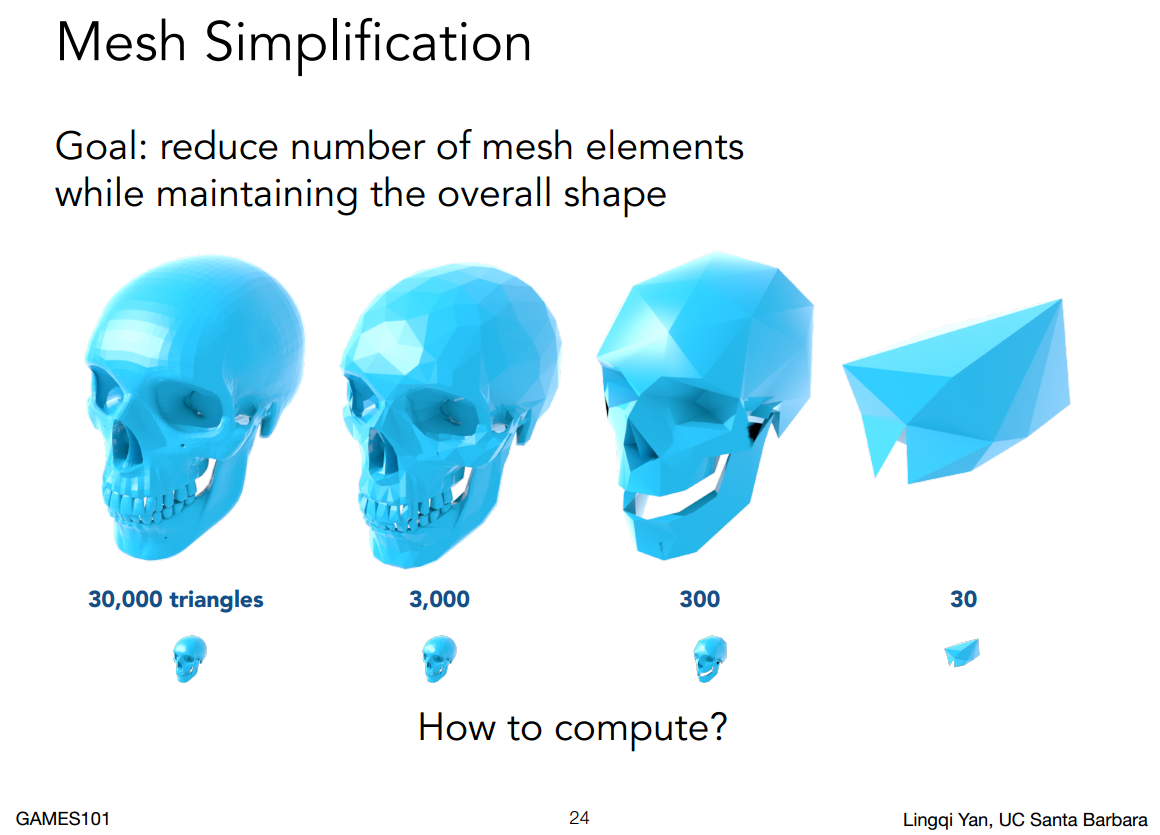
Mesh Simplification 网格简化

网格简化常用于减少顶点数，减轻计算量，优化移动端性能表现，又或者不需要细节表现的场景中使用（比如缩小、远距）。但是几何的层次结构变化可能不如图像层次结构变化来得简单（比如mipmap技术）。

• Edge Collapsing 边坍缩：一种贪心算法，计算所有边坍缩后的二次误差，取二次误差最小的边进行坍缩，坍缩后重新计算更新受影响的边的二次误差值，再取最小进行坍缩。

Shadow 阴影

• umbra: 本影/硬阴影，影子中光源完全照射不到的部分。理想的点光源，不考虑光源自身体积，则只会生成硬阴影
• penumbra: 半影/软阴影，黑暗与光明之间的区域。考虑光源体积则会生成硬阴影与软阴影

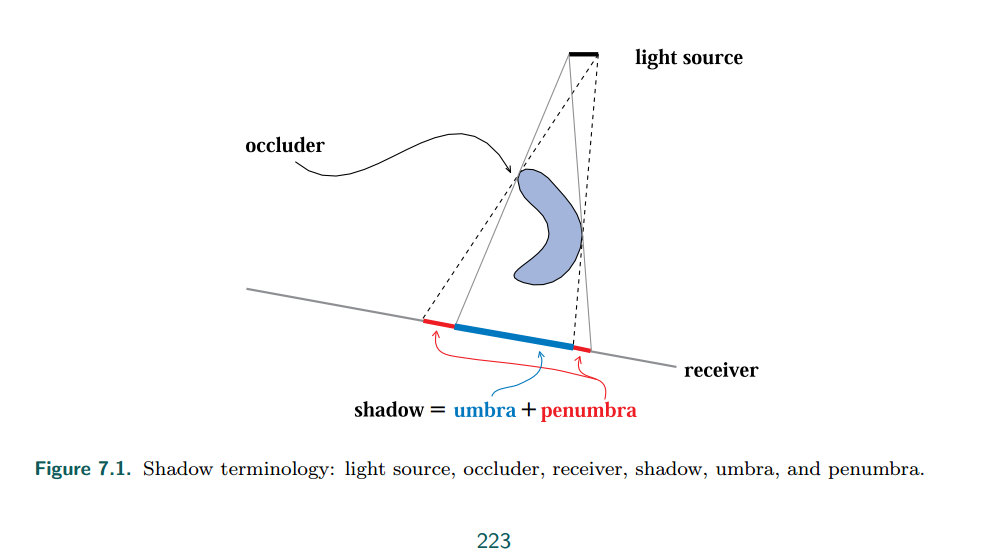
光栅化着色阶段考虑每个着色点时都是进行局部的计算，并没有考虑着色点到光源之间是否有其他物体或物体其他部分阻挡。所以无法计算阴影，由此在光栅化中引入了Shadow Map用来计算阴影。

Shadow Mapping 阴影图/映射

Shadow Mapping仅用于理想点光源/平行光源，原理是

1. 先把一个虚拟相机放在光源位置，做一遍光栅化并生成深度图，用于记录能看到的位置及其深度
2. 然后再通过真实相机做一遍光栅化，着色时将着色点投影回（Reprojected）虚拟相机中，可以求得其在深度图中对应的坐标
3. 将着色点在虚拟相机的深度与深度图中对应坐标的深度比较，二者深度一致表明着色点可见，不一致则说明在阴影中

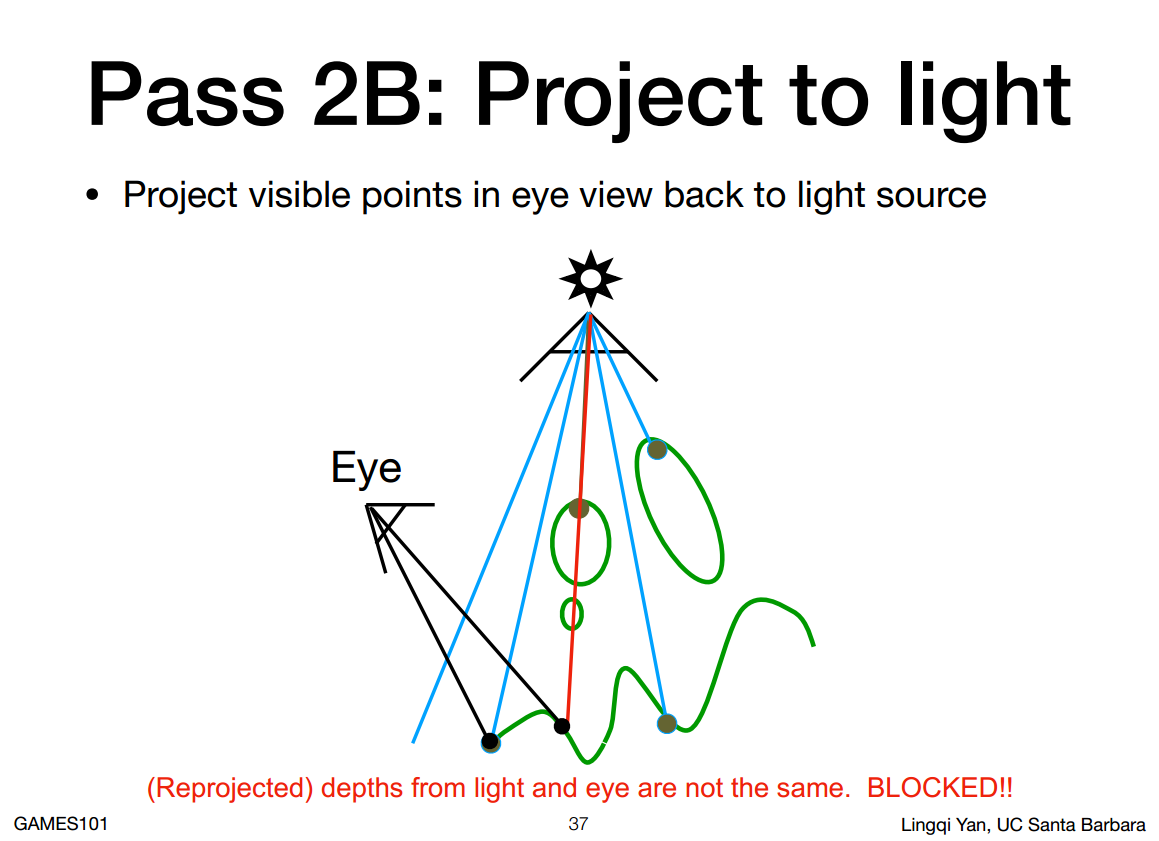
Shadow Mapping存在精度问题，来源于

1. 浮点数本身精度问题
2. 真实相机中的一个像素可能覆盖实际物体的多个点
3. 深度图分辨率问题，生成多少像素的深度图（走样问题）

尽管存在精度问题，需要渲染两遍场景，有额外开销，且只能渲染硬阴影，但Shadow Mapping仍然为一个主流的渲染技术，广泛应用于早期动画以及当下几乎所有3D游戏中（塞尔达荒野之息、马里奥奥德赛）。